Edvancer's Knowledge Hub
How to evaluate a machine learning model – part 2
This blog post is the continuation of my previous post on evaluating a machine learning model.
AUC
AUC is an acronym for area under the curve. Here, the curve is the receiver operating characteristic curve, or ROC curve for short. This seemingly complex name originated in the 1950s from radio signal analysis, and was made popular by Charles Metz in his paper titled “Basic Principles of ROC Analysis” in 1978. The ROC curve plots the rate of true positives to the rate of false positives to show the sensitivity of the classifier. In other words, it shows you the number of correct positive classifications that can be gained as you allow for more and more false positives. The perfect classifier that makes no mistakes would hit a true positive rate of 100% immediately, without incurring any false positives. However, this rarely happens in practice.
 Figure 2-2. Sample ROC curve (source: Wikipedia)
The ROC curve is not just one, single number; it is a whole curve. It provides nuanced details about the behavior of the classifier, but it is difficult to quickly compare many ROC curves to each other. In particular, if one were to employ some kind of automatic hyper parameter-tuning mechanism, the machine would require a quantifiable score instead of a plot that requires visual inspection. The AUC is one way to condense the ROC curve into a single number, so that it can be compared easily and automatically.
Typically, a good ROC curve has ample space under it because the true positive rate shoots up to 100% very quickly. On the other hand, a bad ROC curve covers very little area. Therefore, high AUC is good while low AUC is not.
Outside of the machine learning and datascience community, there are many popular variations of the idea of ROC curves. Those in the marketing analytics community use lift and gain charts. The medical modeling community often looks at odds ratios, whereas the statistics community examines sensitivity and specificity.
Ranking Metrics
We’ve arrived at ranking metrics. But hold up! We are not quite out of the classification jungle yet. One of the primary ranking metrics,precision-recall, is also popular for classification tasks.
Ranking is related to binary classification. Let’s take the example of internet searches. The search engine acts as a ranker. When the user types in a query, the search engine returns a ranked list of webpages that it considers being relevant to the query. Conceptually, one can think of the task of ranking as first a binary classification of “relevant to the query” versus “irrelevant to the query”, followed by ordering the results so that the most relevant items appear at the top of the list. In an underlying implementation, the classifier may assign a numeric score to each item instead of a definite class label based on category, and the ranker may simply order the items by the raw score.
Another example of a ranking problem is personalized recommendation.
The recommender might act either as a ranker or a score-predictor. The output for the first case, is a ranked list of items for each user, while in the case of score prediction, the recommender needs to return a predicted score for each user-item pair. This is an example of a regression model,
Precision-Recall
Precision and recall are two separate metrics which are often used together. Precision answers the question, “Out of the items that the ranker/classifier predicted to be relevant, how many are truly relevant?”
Recall answers the question, “Out of all the items that are truly relevant, how many were found by the ranker/classifier?”
Mathematically, precision and recall can be defined as the following:
Precision = #happy correct answers/ #total items returned by ranker
Recall = #happy correct answers/ #total relevant items
Frequently, one might look at the top k items from the ranker, where k = 5, 10, 20, 100, etc. Then the metrics would be called “precision@k” and “recall@k.”
When dealing with a recommender, there are multiple “queries” of interest; each user is a query into the pool of items. In this case, we can average the precision and recall scores for each query and look at “average precision@k” and “average recall@k.” (This is comparable to the relationship between accuracy and average per-class accuracy for classification.)
Precision-Recall Curve and the F1 Score
When we change k, it results in a change in the number of answers returned by the ranker, and the precision and recall scores. By plotting precision versus recall over a range of k values, we get the precision-recall curve. This is closely related to the ROC curve.
(Here’s a small exercise for the curious reader: What’s the relationship between precision and thefalse-positive rate? What about recall?)
Just like it’s difficult to compare ROC curves to each other, it is also not easy to compare the precision-recall curves. One way of summarizing the precision-recall curve is to fix k and combine precision and recall.
Amongst other methods, these two numbers can be combined via their harmonic mean:
F1 = 2 (precision * recall)/ (precision + recall)
Unlike the arithmetic mean, the harmonic mean leans toward the smaller of the two elements. Hence the F1 score will be small if either precision or recall is small.
Figure 2-2. Sample ROC curve (source: Wikipedia)
The ROC curve is not just one, single number; it is a whole curve. It provides nuanced details about the behavior of the classifier, but it is difficult to quickly compare many ROC curves to each other. In particular, if one were to employ some kind of automatic hyper parameter-tuning mechanism, the machine would require a quantifiable score instead of a plot that requires visual inspection. The AUC is one way to condense the ROC curve into a single number, so that it can be compared easily and automatically.
Typically, a good ROC curve has ample space under it because the true positive rate shoots up to 100% very quickly. On the other hand, a bad ROC curve covers very little area. Therefore, high AUC is good while low AUC is not.
Outside of the machine learning and datascience community, there are many popular variations of the idea of ROC curves. Those in the marketing analytics community use lift and gain charts. The medical modeling community often looks at odds ratios, whereas the statistics community examines sensitivity and specificity.
Ranking Metrics
We’ve arrived at ranking metrics. But hold up! We are not quite out of the classification jungle yet. One of the primary ranking metrics,precision-recall, is also popular for classification tasks.
Ranking is related to binary classification. Let’s take the example of internet searches. The search engine acts as a ranker. When the user types in a query, the search engine returns a ranked list of webpages that it considers being relevant to the query. Conceptually, one can think of the task of ranking as first a binary classification of “relevant to the query” versus “irrelevant to the query”, followed by ordering the results so that the most relevant items appear at the top of the list. In an underlying implementation, the classifier may assign a numeric score to each item instead of a definite class label based on category, and the ranker may simply order the items by the raw score.
Another example of a ranking problem is personalized recommendation.
The recommender might act either as a ranker or a score-predictor. The output for the first case, is a ranked list of items for each user, while in the case of score prediction, the recommender needs to return a predicted score for each user-item pair. This is an example of a regression model,
Precision-Recall
Precision and recall are two separate metrics which are often used together. Precision answers the question, “Out of the items that the ranker/classifier predicted to be relevant, how many are truly relevant?”
Recall answers the question, “Out of all the items that are truly relevant, how many were found by the ranker/classifier?”
Mathematically, precision and recall can be defined as the following:
Precision = #happy correct answers/ #total items returned by ranker
Recall = #happy correct answers/ #total relevant items
Frequently, one might look at the top k items from the ranker, where k = 5, 10, 20, 100, etc. Then the metrics would be called “precision@k” and “recall@k.”
When dealing with a recommender, there are multiple “queries” of interest; each user is a query into the pool of items. In this case, we can average the precision and recall scores for each query and look at “average precision@k” and “average recall@k.” (This is comparable to the relationship between accuracy and average per-class accuracy for classification.)
Precision-Recall Curve and the F1 Score
When we change k, it results in a change in the number of answers returned by the ranker, and the precision and recall scores. By plotting precision versus recall over a range of k values, we get the precision-recall curve. This is closely related to the ROC curve.
(Here’s a small exercise for the curious reader: What’s the relationship between precision and thefalse-positive rate? What about recall?)
Just like it’s difficult to compare ROC curves to each other, it is also not easy to compare the precision-recall curves. One way of summarizing the precision-recall curve is to fix k and combine precision and recall.
Amongst other methods, these two numbers can be combined via their harmonic mean:
F1 = 2 (precision * recall)/ (precision + recall)
Unlike the arithmetic mean, the harmonic mean leans toward the smaller of the two elements. Hence the F1 score will be small if either precision or recall is small.
Share this on





Follow us on




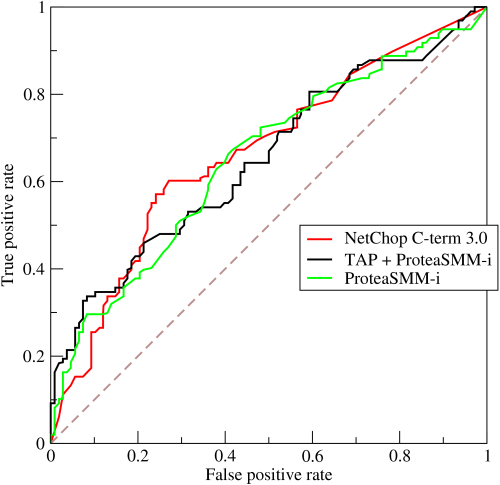 Figure 2-2. Sample ROC curve (source: Wikipedia)
The ROC curve is not just one, single number; it is a whole curve. It provides nuanced details about the behavior of the classifier, but it is difficult to quickly compare many ROC curves to each other. In particular, if one were to employ some kind of automatic hyper parameter-tuning mechanism, the machine would require a quantifiable score instead of a plot that requires visual inspection. The AUC is one way to condense the ROC curve into a single number, so that it can be compared easily and automatically.
Typically, a good ROC curve has ample space under it because the true positive rate shoots up to 100% very quickly. On the other hand, a bad ROC curve covers very little area. Therefore, high AUC is good while low AUC is not.
Outside of the machine learning and datascience community, there are many popular variations of the idea of ROC curves. Those in the marketing analytics community use lift and gain charts. The medical modeling community often looks at odds ratios, whereas the statistics community examines sensitivity and specificity.
Ranking Metrics
We’ve arrived at ranking metrics. But hold up! We are not quite out of the classification jungle yet. One of the primary ranking metrics,precision-recall, is also popular for classification tasks.
Ranking is related to binary classification. Let’s take the example of internet searches. The search engine acts as a ranker. When the user types in a query, the search engine returns a ranked list of webpages that it considers being relevant to the query. Conceptually, one can think of the task of ranking as first a binary classification of “relevant to the query” versus “irrelevant to the query”, followed by ordering the results so that the most relevant items appear at the top of the list. In an underlying implementation, the classifier may assign a numeric score to each item instead of a definite class label based on category, and the ranker may simply order the items by the raw score.
Another example of a ranking problem is personalized recommendation.
The recommender might act either as a ranker or a score-predictor. The output for the first case, is a ranked list of items for each user, while in the case of score prediction, the recommender needs to return a predicted score for each user-item pair. This is an example of a regression model,
Precision-Recall
Precision and recall are two separate metrics which are often used together. Precision answers the question, “Out of the items that the ranker/classifier predicted to be relevant, how many are truly relevant?”
Recall answers the question, “Out of all the items that are truly relevant, how many were found by the ranker/classifier?”
Mathematically, precision and recall can be defined as the following:
Precision = #happy correct answers/ #total items returned by ranker
Recall = #happy correct answers/ #total relevant items
Frequently, one might look at the top k items from the ranker, where k = 5, 10, 20, 100, etc. Then the metrics would be called “precision@k” and “recall@k.”
When dealing with a recommender, there are multiple “queries” of interest; each user is a query into the pool of items. In this case, we can average the precision and recall scores for each query and look at “average precision@k” and “average recall@k.” (This is comparable to the relationship between accuracy and average per-class accuracy for classification.)
Precision-Recall Curve and the F1 Score
When we change k, it results in a change in the number of answers returned by the ranker, and the precision and recall scores. By plotting precision versus recall over a range of k values, we get the precision-recall curve. This is closely related to the ROC curve.
(Here’s a small exercise for the curious reader: What’s the relationship between precision and thefalse-positive rate? What about recall?)
Just like it’s difficult to compare ROC curves to each other, it is also not easy to compare the precision-recall curves. One way of summarizing the precision-recall curve is to fix k and combine precision and recall.
Amongst other methods, these two numbers can be combined via their harmonic mean:
F1 = 2 (precision * recall)/ (precision + recall)
Unlike the arithmetic mean, the harmonic mean leans toward the smaller of the two elements. Hence the F1 score will be small if either precision or recall is small.
Figure 2-2. Sample ROC curve (source: Wikipedia)
The ROC curve is not just one, single number; it is a whole curve. It provides nuanced details about the behavior of the classifier, but it is difficult to quickly compare many ROC curves to each other. In particular, if one were to employ some kind of automatic hyper parameter-tuning mechanism, the machine would require a quantifiable score instead of a plot that requires visual inspection. The AUC is one way to condense the ROC curve into a single number, so that it can be compared easily and automatically.
Typically, a good ROC curve has ample space under it because the true positive rate shoots up to 100% very quickly. On the other hand, a bad ROC curve covers very little area. Therefore, high AUC is good while low AUC is not.
Outside of the machine learning and datascience community, there are many popular variations of the idea of ROC curves. Those in the marketing analytics community use lift and gain charts. The medical modeling community often looks at odds ratios, whereas the statistics community examines sensitivity and specificity.
Ranking Metrics
We’ve arrived at ranking metrics. But hold up! We are not quite out of the classification jungle yet. One of the primary ranking metrics,precision-recall, is also popular for classification tasks.
Ranking is related to binary classification. Let’s take the example of internet searches. The search engine acts as a ranker. When the user types in a query, the search engine returns a ranked list of webpages that it considers being relevant to the query. Conceptually, one can think of the task of ranking as first a binary classification of “relevant to the query” versus “irrelevant to the query”, followed by ordering the results so that the most relevant items appear at the top of the list. In an underlying implementation, the classifier may assign a numeric score to each item instead of a definite class label based on category, and the ranker may simply order the items by the raw score.
Another example of a ranking problem is personalized recommendation.
The recommender might act either as a ranker or a score-predictor. The output for the first case, is a ranked list of items for each user, while in the case of score prediction, the recommender needs to return a predicted score for each user-item pair. This is an example of a regression model,
Precision-Recall
Precision and recall are two separate metrics which are often used together. Precision answers the question, “Out of the items that the ranker/classifier predicted to be relevant, how many are truly relevant?”
Recall answers the question, “Out of all the items that are truly relevant, how many were found by the ranker/classifier?”
Mathematically, precision and recall can be defined as the following:
Precision = #happy correct answers/ #total items returned by ranker
Recall = #happy correct answers/ #total relevant items
Frequently, one might look at the top k items from the ranker, where k = 5, 10, 20, 100, etc. Then the metrics would be called “precision@k” and “recall@k.”
When dealing with a recommender, there are multiple “queries” of interest; each user is a query into the pool of items. In this case, we can average the precision and recall scores for each query and look at “average precision@k” and “average recall@k.” (This is comparable to the relationship between accuracy and average per-class accuracy for classification.)
Precision-Recall Curve and the F1 Score
When we change k, it results in a change in the number of answers returned by the ranker, and the precision and recall scores. By plotting precision versus recall over a range of k values, we get the precision-recall curve. This is closely related to the ROC curve.
(Here’s a small exercise for the curious reader: What’s the relationship between precision and thefalse-positive rate? What about recall?)
Just like it’s difficult to compare ROC curves to each other, it is also not easy to compare the precision-recall curves. One way of summarizing the precision-recall curve is to fix k and combine precision and recall.
Amongst other methods, these two numbers can be combined via their harmonic mean:
F1 = 2 (precision * recall)/ (precision + recall)
Unlike the arithmetic mean, the harmonic mean leans toward the smaller of the two elements. Hence the F1 score will be small if either precision or recall is small.
Manu Jeevan
Manu Jeevan is a self-taught data scientist and loves to explain data science concepts in simple terms. You can connect with him on LinkedIn, or email him at manu@bigdataexaminer.com.
Latest posts by Manu Jeevan (see all)
- Python IDEs for Data Science: Top 5 - January 19, 2019
- The 5 exciting machine learning, data science and big data trends for 2019 - January 19, 2019
- A/B Testing Made Simple – Part 2 - October 30, 2018
Follow us on
Free Data Science & AI Starter Course

